Legendre Polynomials & Spherical Harmonics

The angular part of the Laplacian Operator in spherical coordinates is

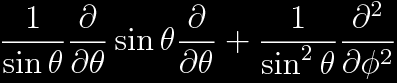
The conversion of the Laplacian operator from Cartesian to spherical coordinates can be found elsewhere.

Many problems are azimuthally symmetric. For the sake of simplicity, first ignore φ and concentrate on the θ part.

A substitution greatly simplifies the equation.

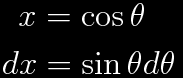
Use the chain rule to rewrite the differential equation.

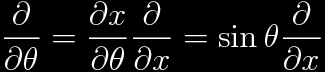
This x is not to be confused with a spatial coordinate. The θ operator becomes

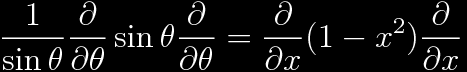
The goal is to find eigenfunctions of this operator. Call them P_l(x).

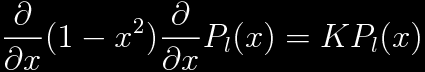
Substitute a power series for P_l(x).

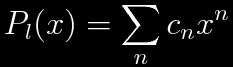
Substitution into the differential equation yields

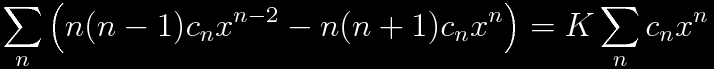
The recursion relationship between the coefficients is

Each P_l(x) should be well behaved for values of x from -1 to 1. To be sure that the series does not diverge, assume that there is a maximum value of n for which c_n is not zero. Call this value l. The recursion relationship between l+2 and l becomes

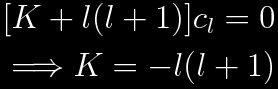
The value of all the c_n can be found in terms of c_l from a recursion relation.

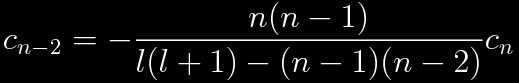
The series will always terminate with c₁ or c₀, depending on whether l is odd or even. The equation above can be used to relate all the coefficients, then normalization will give the overall amplitude. Now consider the first two terms, l-2 and l-4.

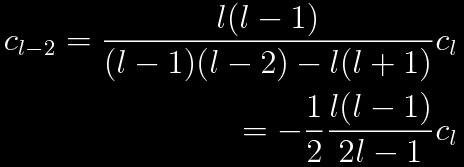
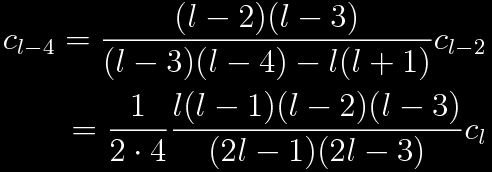
Indeed, there is a pattern.

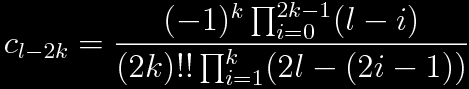
Associated Legendre Polynomials and Spherical Harmonics

The angular portion of the Laplacian operator, written in terms of x=cos(θ), is

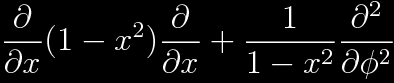
Assuming a φ dependence of exp(imφ), the eigenfunctions associated with θ should satisfy the equation

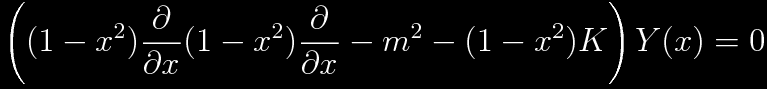
But this equation is not the whole story. Another equation can be written in terms of y²=1-x². Once again, this is not to be confused with a spatial coordinate. This is a differential equation in terms of sin(θ).

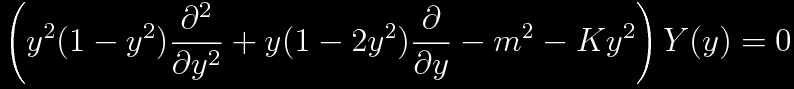
Any value of m must be an integer, so that azimuthal rotations by 360° do not change anything. Now make another trusty power-series substitution

The differential equations can be solved by recursion.

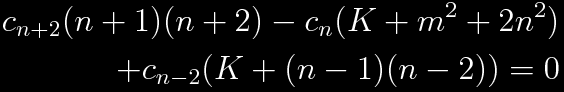
Once again, for the sake of convergence, consider solutions that have a maximum value of n for which c_n is nonzero. Call this value l again, then setting n-2=l in the recursive formulae, once again the result is

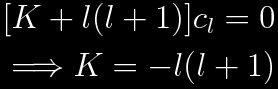
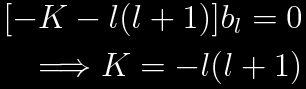
Now consider the recursion relation from the y equation. The equation in terms of x is more complicated and there is a better way to find the corresponding solutions.

Since l determines the highest nonzero coefficient of the power series, it is convenient to solve for the lower coefficients in terms of the higher coefficients.

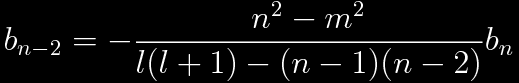
There must be a minimum value of n; otherwise, the series will diverge at y=0. Given l, for the series to converge, it is necessary that |m|=l-2k, with k greater than or equal to zero and less than or equal to l/2. For even or odd l, this series gives l+1 solutions. This solution gives the eigenfunctions with both odd or both even m and l.

Finally, it is time to find the remaining solutions more effectively. To this end, make another substitution.

Now find the derivatives. The first derivative:

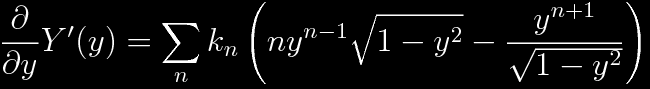
The second derivative:

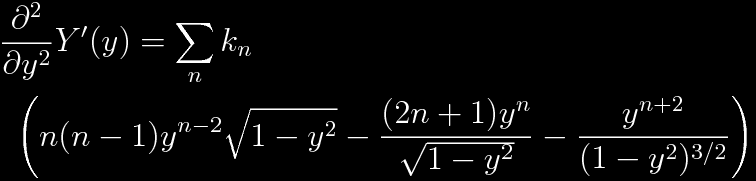
Putting the derivatives into the differential equations yields

The new recursion relation is

This time, suppose the highest term in the series is k_l-1. Then one finds the usual value of K.

The relationship between coefficients is then

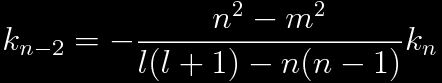
In this case, the maximum value of n is l-1. For odd l, this equation yields convergent solutions for even values of |m| from 0 to l-1. For even l, this equation yields convergent solutions for odd values of |m| from 1 to l-1.

A total of 2l+1 solutions have been found for a given l. This bodes well for finding wavefunctions of the Hydrogen atom.