The Gamma Function

The gamma function is a generalized version of the factorial function.

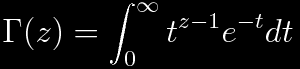
The gamma function comes in many forms. This integral representation is nice because the connection with factorials can be made quickly with integration by parts. (Γ(z)=(z-1)!)

It is sometimes useful to evaluate the Γ function in the form of an infinite product. To obtain this form, first insert a defnition of e.

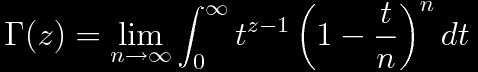
Then substitute s=t/n.

Then integrate by parts.

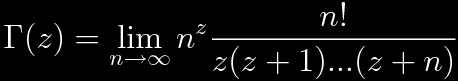
Factor n! from the denominator.

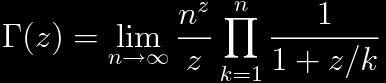
Rewrite n^z as the exponential of a logarithm and factor an exponential in terms of the Euler-Mascheroni constant.

The following definition of the Euler-Mascheroni constant has been used.

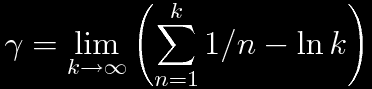
Why bother? Now it's quite easy to evaluate the Γ function in some circumstances. For example, consider an imaginary number iy.

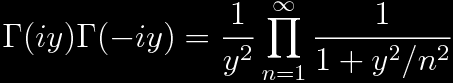
Used in conjunction with the following product for the sine function,

,

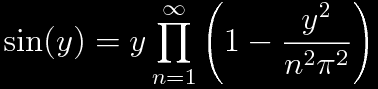the product becomes

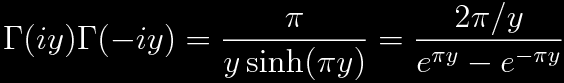
This result is closely related to Euler's reflection formula.